1. 이진 탐색(Binary Search)
보통 우리가 탐색을 시도할 때는 순차적으로 탐색하는 방법을 이용한다. 기존의 순차 탐색은 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 하나씩 데이터를 확인하는 방법이다. 리스트에서 특정 데이터를 찾기 위해 검사할 때, 별 다른 조건이 없으면 순차적으로 탐색을 시도한다.
이와 달리 이진 탐색은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다. 여기서 전제는 탐색하려는 리스트가 정렬되어 있어야 한다는 점이다!
이진 탐색을 하기 위해서는 탐색 범위를 설정해줘야 하는데, 총 세 가지 포인트가 있다.
- 시작점 (start)
- 끝점 (end)
- 중간점 (mid = (start+end)//2)
이 셋을 이용해 탐색한다.
순서는 아래와 같다.
- 시작점과 끝점을 전체 리스트의 양 끝으로 설정한 다음, 중간점을 찾는다.
- 위치를 찾고자 하는 값(=target)과 중간값의 크기를 비교해, 중간값이 더 크면 target이 시작점과 중간값 사이에 위치해있다는 뜻이므로, 시작점은 그대로 두고 끝점을 중간점 바로 한 칸 아래로 옮긴다(start, end) => (start, mid - 1)
- 반대로 target이 중간값보다 크다면 target은 중간값과 끝점 사이에 위치해있다는 뜻이므로 끝점은 그대로 두고 시작점을 중간점 바로 한 칸 위로 옮긴다.(start, end) => (mid + 1, end)
이진 탐색을 배우자마자 떠오른 개념이 하나 있었다.

업다운 게임!
술자리에서 병뚜껑 업다운 게임할 때 시작부터 꼭 10! 이딴 거 외치는 애들 이해가 되지 않았는데, 이미 그때부터 이진 탐색을 체화하고 있던 게 아닌가 싶다.
보다 이해를 돕기 위해 예시 문제를 하나 풀어보자. 출처는 나동빈님 유튜브 영상에서 가져왔다.
문제: 이미 정렬된 10개의 데이터 중 값이 4인 원소의 위치를 찾는 문제

시작하는 시점에서 시작점, 끝점, 중간점은 각각 0, 9, 4이다. (인덱스 값)
중간점이 4인 이유는, (0+9)를 2로 나눈 몫을 취하기 때문(정수 값을 얻기 위해)이다.

위에서 말했듯, 정렬되어 있는 리스트에서 중간점과 위치를 찾고 싶은 값(4)를 비교해 찾고 싶은 값이 더 작다면, 중간점부터 끝점까지 리스트는 굳이 확인할 필요가 없음. 오른쪽 값은 전부 중간점보다 클테니. 그래서 리스트가 정렬되어 있어야 함.
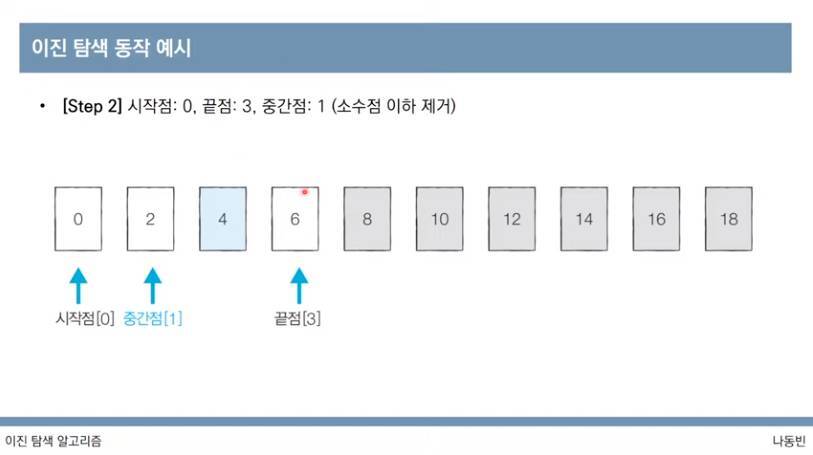
여기서는 중간점보다 값이 크기 때문에 시작점을 중간점 오른쪽으로 옮긴다.

찾고자 하는 값인 4가 시작점&중간점을 같이 가지기에 이로부터 최종값을 도출할 수 있음.
이분 탐색의 시간 복잡도
단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 log2 n에 해당된다. (O(logN))
ex)
- 초기 데이터 개수가 32개일 때, 이상적으로 1단계만큼의 시간을 거치면 절반인 16개 가량의 데이터가 남는다.
- 여기서 한 단계(2단계)만큼의 시간 더 거치면 절반인 8개 가량의 데이터가 남는다.
- 여기서 또 거치면 (3단계) 4개가 남는다.
각 단계에 해당하는 데이터 양(N)이 절반씩 줄어드는데 한 단계 당 log2(N)만큼의 시간이 소요되는 것을 알 수 있다.
1단계: 데이터 수(N) = 32, 해당 단계의 시간 인덱스: log2(32) = 5
(5분, 5시간이라는 뜻이 아니라 그냥 정해진 시간 개념. 걍 5시라고 하자.)
2단계: N = 16, log2(16) = 4
3단계: N = 8, log2(8) = 3
4단계: N = 4, log2(4) = 2
5단계: N = 2, log2(2) = 1
다음 단계로 1만큼의 시간이 이동하는데 데이터가 절반씩 줄어드니 log2N이다.
이진 탐색 코드 구현
이진 탐색을 구현할 때는 반드시 종료 조건이 필요하다. start와 end가 점점 가까워지다가 더 이상 사이에 값이 없을 때를 지나면 start > end가 된다. 이를 종료 조건으로 설정하는 것이 일반적이다.
예시
#재귀
def binary_search(array, target, start, end): # 주의! start, end는 모두 인덱스를 뜻함/
if start > end: # 종료 조건
return None
mid = (start + end) // 2 (중간점에 해당하는 인덱스)
if array[mid] == target:
return mid (target에 해당하는 인덱스를 찾았으므로 mid 인덱스 반환)
elif array[mid] > target:
return binary_search(array, target, start, mid-1) # target이 mid보다 작은 곳에 있으니 end를 mid 바로 아래로 옮긴다.
else:
return binary_search(array, target, mid+1, end)
2. 파라메트릭 서치
오늘 나를 애먹였던 애들이 전부 여기에 해당했다. 싹다 파라메트릭 서치 문제. 한 문제 열심히 끙끙대다가 도저히 안 풀려서 설명 보면 아하! 이래서 이분 탐색이구나! 하고 다른 파라메트릭 서치 건드리면 또 끙끙.. 아직 파라메트릭 서치에 대한 개념이 잘 탑재되지 않은 것 같다. TIL을 정리하면서 다시금 개념을 익혀보자.
파라메트릭 서치란 최적화 문제를 결정 문제("예" 혹은 "아니오")로 바꾸어 해결하는 기법이다. 예시로는 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제를 풀기에 적합하다.
코딩 테스트에서는 보통 주어진 입력값의 범위가 매우 길 때 (10억이라던지 그 이상), 이 모든 걸 탐색해서 최적값을 찾아내야 하는 문제라면 반드시 이진 탐색을 떠올리도록 하자.
오늘 내가 푼 문제는 두 가지이다.
- 떡볶이 떡 문제(=나무 자르기)
- 공유기 설치
1. 떡볶이 떡 문제 (=나무 자르기)
떡볶이 떡은 나동빈님 강의에서 나왔던 문제의 제목으로, 백준에서는 나무 자르기로 나온다. 둘다 문제의 구성과 제출 답안 역시 완전히 똑같으니 뭘 봐도 상관없다. 아래 코드에서는 나무를 떡으로 생각했기에 rice_cakes라는 리스트 이름이 들어간다.
이 문제의 해결 아이디어는 다음과 같다.
- 적절한 높이를 찾을 떄까지 이진 탐색을 수행하여 높이 H를 반복해서 조정한다.
- '현재 이 높이로 자르면 조건을 만족할 수 있는가?'를 확인한 뒤에, 조건의 만족 여부("예" 혹은 "아니오")에 따라서 탐색 범위를 좁혀서 해결할 수 있다.
- 절단기의 높이는 0에서부터 10억까지의 정수 중 하나다.
- 이렇게 큰 탐색 범위를 보면 가장 먼저 이진 탐색을 떠올려야 한다는 점! 필수!!!
예시 그림을 살펴보자. 높이의 최대값을 구하는 문제이기 때문에, 최대값인지 알려면 계속해서 결과를 저장해둬야 한다.

위 이미지처럼, 모든 나무(a.k.a. 떡볶이)의 시작점은 0으로 동일하다. 하지만 각자 높이가 다른데, 이 중 가장 길이가 긴 떡의 길이를 끝점으로 잡는다. 그러면 중간점을 구할 수 있다. 떡의 길이가 담겨 있는 리스트를 rice_cakes라 하면
start = 0
end = max(rice_cakes)
mid = (start+end) // 2
이다. 여기서 잘린 떡의 길이는 각각 rice_cakes[i]-mid일텐데, 이를 모두 다 더한 총합과 문제에서 주어진 최소 떡의 양 M을 비교한다. M보다 크면, 떡의 길이를 덜 잘라도 된다는 말이니 중간점을 올려야 한다. (start => mid + 1) 이때, 중간점을 올리는 순간 거기에서 나올 떡의 총량은 무조건 이전 총량보다는 적을 것이기에 다음 페이즈로 넘어갈 때는 굳이 저장하지 않아도 된다.
이런 식으로 중간점이 오르내리다가 최적값에 도달하면 종료하는 방식으로 진행된다.
코드는 아래와 같다. 크게 두 가지 방식을 짰는데, 첫번째는 while문을 이용해 순수하게 반복문으로 짰고, 다음은 재귀를 활용했다.
여기서 개꿀팁!! 내일 공부 내용에 적을 것인데, 아래 반복문은 원래 정답 제출했을 때 계속 시간 초과가 떴던 코드였다. 처음에 제출할 때 코드는 아래와 같이 함수로 정의하지 않고 그냥 주루룩 적어서 풀었는데, 반면 아래와 같이 binary_search라는 함수를 선언하고 실행하니 정답으로 통과되는 것을 확인했다!!
내일 정리할 것이지만, 미리 아래 링크를 참조하면 도움이 될 것이다. 검색 키워드는 "python 함수 더 빠른 이유"
글 읽기 - 나무자르기 함수로 빼면왜 시간초과가 안날가요..
댓글을 작성하려면 로그인해야 합니다.
www.acmicpc.net
아래는 정답으로 제출한 코드이다. 두 가지 풀이를 적었다.
1. 반복문(while문)을 활용한 코드
# Solution 1: 반복문
start = 0
end = max(rice_cakes)
# 재귀에 너무 목숨걸지 말자..!
ans = 0
def binary_search(array, start, end):
while (start <= end):
total_amount = 0
mid = (start + end) // 2
for i in rice_cakes:
if i > mid:
total_amount += i - mid
if total_amount < M:
end = mid-1
else:
ans = mid
start = mid + 1
print(ans)
binary_search(rice_cakes, start, end)
2. 재귀를 활용한 코드.
from sys import stdin
def binary_search(rice_cakes, target, start, end):
total_cakes = 0
mid = (start + end) // 2
# 종료 조건
if start > end:
print(mid)
return
for i in rice_cakes:
if i > mid:
total_cakes += i - mid
if total_cakes >= target:
binary_search(rice_cakes, target, mid + 1, end)
elif total_cakes < target:
binary_search(rice_cakes, target, start, mid - 1)
N, M = map(int, stdin.readline().split())
rice_cakes = list(map(int, stdin.readline().split()))
start = 0
end = max(rice_cakes)
while True:
a = binary_search(rice_cakes, M, start, end)
if a == None:
break2. 공유기 설치 문제
다음은 공유기 설치 문제였다. 기분 좋게 떡 문제를 해결하고 나서 다음 문제를 잡은 게 공유기였는데, 여기서 시간을 너무 많이 써버렸다...혼자서 엄청 오래 끙끙대다가 도저히 안되겠어서 풀이를 검색해 참조했는데도 도저히 모르겠더라.
내가 가장 이해되지 않았던 개념은
1) start, mid, end라는 값이 정확히 무엇을 지칭하는지. 이전 문제나 이진 탐색 문제를 풀 때는 이 start, mid, end로 리스트에서 양끝과 중간점의 인덱스를 쓰는 것으로 이해했는데 여기서는 아니었다. 여기서는 공유기 간 거리의 최소값(start)과 최대값(end)으로 지정해야 문제가 풀렸다. 이를 이해하는데 가장 많이 도움이 된 풀이는 여기서였다. (이 블로그에서도 병뚜껑 업다운 얘기하니 So 반갑 ㅎㅁㅎ)
문제를 잘 읽어야겠다. 우리가 찾아야 하는 건 "가장 인접한 두 공유기 사이의 거리의 최댓값"이다. 이는 집 리스트 내 value 중 최댓값이 아니라 max((value[i+1]-value[i]) for _ in range(N))에 해당한다. 그러니 start, end, mid 역시 집 리스트 내 value 간 차이값으로 배치되어야 한다.
2) 대체 무엇을 이분해서 조건을 확인하고 갱신하는 건지 도통 모르겠더라. 1)이 이해되지 않으니 당연히 2)도 이해되지 않았다. 어떻게 하면 되냐면, 초기값을 중간값(=mid)으로 설정한다. 맨 왼쪽 집부터 mid 사이 간격으로 차례대로 공유기를 먼저 배치해보고
(집 리스트를 homes라 하면 맨 첫번째 왼쪽 집은 homes[0]이다. 여기서부터 mid 만큼의 거리로 공유기를 설치한다고 가정하면, i 번째 설치한 공유기는 homes[0]에서 mid * (i-1)만큼 떨어져 있을 것이다. 이를 N번 반복하면서 인접한 두 집을 비교하는 식으로 진행한다. 예컨대 실제 집 위치 homes[1]과 homes[0] 사이의 거리가 mid보다 멀다면 => count +=1을 추가한다.
homes[i] - homes[i-1] > mid 이면: 즉, 중간값 거리보다 homes[i]와 homes[i-1] 사이가 더 멀다는 뜻이 된다.
이 때 필요한 공유기 수(=count)와 문제에서 주는 c의 개수를 비교해서 c의 개수가 count보다 적으면 그만큼 집 사이 간격이 mid보다 큰 곳이 많다는 것이니 mid 값을 키워서 문제에서 제공하는 공유기 수 c와 count가 같아질 때가 곧 최대값이 될 것이다.
이를 정리하면
- 가상으로 공유기를 설치하기 위해 두 집 사이 거리로 설정하는 초기값으로 중간값을 세팅한다. 중간값은 두 집 사이 거리의 최솟값 start= 1(두 집 사이에 거리는 반드시 자연수여야 하니 최솟값은 1)부터 최댓값 end=homes[-1] - homes[0]의 중간값이다.
- 이렇게 중간값을 바탕으로 가상으로 설치해본 뒤, 이렇게 설치하는데 필요한 공유기 수와 실제 문제에서 제공하는 공유기 수를 비교해본다. 가상의 공유기 수가 제공받는 공유기 수보다 많다면 mid 거리가 작다는 뜻이니 mid 값을 올린다. 반대로 가상의 공유기 수가 적으면 설정한 중간값이 너무 커서이니 줄여야 한다. 이렇게 진행했을 때 집 사이 간격의 mid가 가장 최적에 도달할 때 그 mid 값이 곧 최대값이 된다.
결국 최대 간격은 최대 중간값에 해당하는 개념이라고 생각하자. 될 수 있는 최대 중간값이 곧 최대 간격이다. 코드는 아래와 같다.
from sys import stdin
n, c = map(int, stdin.readline().split())
homes = [int(stdin.readline()) for _ in range(n)]
homes.sort()
start = 1
end = homes[-1] - homes[0]
result = 0 # 공유기 사이 거리의 최대값
while (start <= end):
mid = (start + end)//2
count = 1
current = homes[0]
for i in range(1, n):
if homes[i] >= current + mid:
count +=1
current = homes[i]
if count >= c: # mid 간격보다 큰 애들이 설치해야 할 공유기 대수 이상이라는 뜻이니 mid 간격을 늘려야. 그러려면 start를 mid+1만큼 올려야 start+end의 평균이 그만큼 올라감.
start = mid + 1
result = mid
else:
end = mid -1
print(result)이렇게 써봤지만 아직도 파라메트릭 서치는 연습이 좀 더 필요할 듯하다. 핵심은
1) 문제에서 찾아야 하는 최적값이 무엇인지를 잘 정의하고
2) 그에 맞게 start, end, mid를 설정해야 하며
3) 이 셋이 인덱스여야 할 필요는 전혀 없다는 점.
'정글사관학교 개발일지 > 자료구조&알고리즘' 카테고리의 다른 글
| 정글사관학교 14일차 TIL: 컴퓨터 시스템 1장 - A Tour of Computer Systems (1-1 ~ 1-4) (0) | 2021.11.15 |
|---|---|
| 정글사관학교 13일차 TIL: 이분 탐색 - 두 용액(투포인터 알고리즘), 가장 긴 증가하는 부분 수열 (1) | 2021.11.14 |
| 정글사관학교 11일차 TIL: 숫자 야구(#2503), 독일 로또(#6603) (0) | 2021.11.12 |
| 정글사관학교 10일차 TIL: 안전 영역 문제 풀이, 정렬 알고리즘 정리(버블 정렬, 선택 정렬, 삽입 정렬, 힙 정렬) (0) | 2021.11.11 |
| 정글사관학교 9일차 TIL: BFS & DFS, 큐와 스택 (0) | 2021.11.10 |