0. 목차
1. 아침 산책 풀이
2. 위상 정렬
점점 말이 없어진다.. 바로 풀이로 가자.
1. 아침 산책 (#21606)
먼저 문제 링크.
문제 풀이의 논리는 아래와 같다.
- 문제에서는 실내 노드에서 출발해 실내 노드로 도착한다고 설명한다. 그래서 실내를 기준으로 생각하게 되나, 이 문제는 실외 노드를 중심에 놓고 인접한 실내 노드를 세는 방식이 훨씬 편하다. 먼저 실외 노드를 기준으로 인접해있는 실내 노드 수를 count한다.
- 실외 노드를 가운데 놓고 인접한 실내 점 n개가 붙어있을 때, 갈 수 있는 경로의 수는 n * n-1 (n개의 실내 점 중 하나 고르는 경우의 수 X 실외 점 1개 고르는 경우의 수 1 X 앞에서 고른 1개의 실내 점 제외한 n-1개 점 중 하나 고르는 경우의 수)
- for문 돌면서 실외 점을 만났는데 해당 점을 아직 방문하지 않았다면 그 점을 기준으로 dfs 재귀를 돌린다.
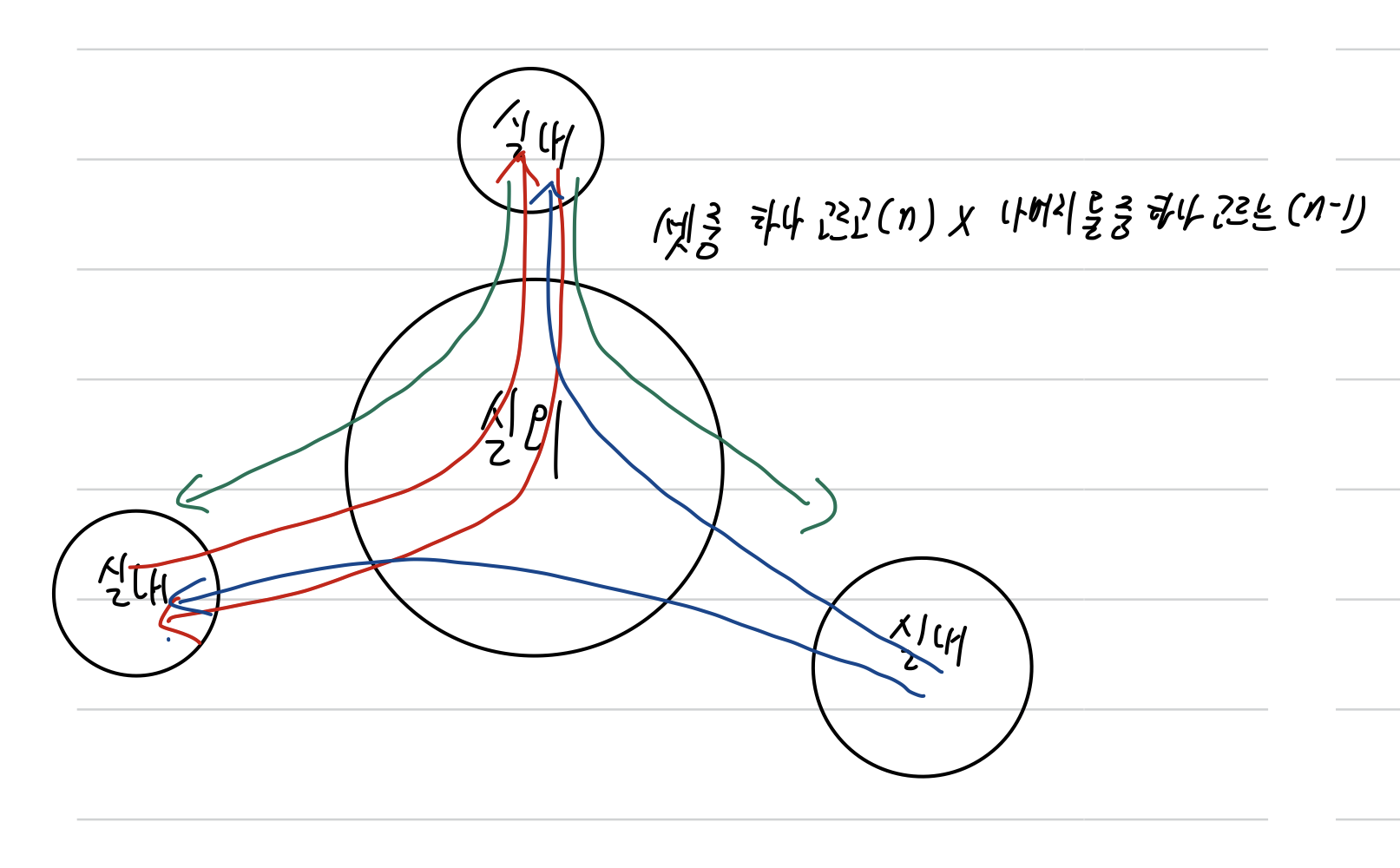
이때 주의해야 할 점이 하나 있는데, 실외 노드끼리 연결되는 경우는 두 가지 케이스가 있다.
1) 실외 노드끼리 인접해서 연결될 때
2) 중간에 실내 노드를 끼고 있을 때(이건 엄밀히 말하면 실외 노드가 연결되었다고 할 수 없으나 주의사항을 위해서)

위의 사항을 고려하면서 dfs를 이용하면 된다.
마지막으로 한 가지 더 고려해야 할 점! 처음에 입력값을 받아올 때, 주어진 점 둘 다 실내라면 => 즉, 실내끼리 인접해서 연결되어 있다면 실내(a, b)에서 출발해 실내(b, a)에서 끝나는 경우 2가지를 추가해야 한다. 따라서 이때 +2를 더해준다.
최종 코드는 아래와 같다.
from sys import setrecursionlimit, stdin
setrecursionlimit(10**9)
"""문제 풀이 논리
1. 실외 점을 기준으로 인접해있는 실내 노드 개수를 count한다.
2. 실외 점을 중간에 놓고 실내 점 n개가 붙어있을 때 갈 수 있는 경로의 수는 n * 1(중간 실외 점 선택) * (n-1) = n*(n-1)에 해당.
3. 실외 노드끼리 연결되는 경우는 1) 실외끼리 인접 노드로 연결될 때 2) 중간에 실내 노드를 끼고 연결할 때. 이를 분리해서 생각.
"""
def dfs(v, cnt): # v: 정점 번호 & cnt: 실외와 연결된 실내 노드 개수 카운트
visited[v] = True
for i in graph[v]: # 노드 v와 연결된 인접 노드를 하나씩 불러온다.
if location[i] == 1: # 해당 노드의 위치가 실내이면
cnt += 1 # 실내 개수 카운트에 +1을 해준다
elif not visited[i] and location[i] == 0: # 방문하지 않고 해당 i 점의 위치가 실외이면
cnt = dfs(i, cnt) # 해당 실외 점을 기준으로 dfs를 돈다!
return cnt
ans = 0
n = int(stdin.readline()) # 정점 수 받기
location = [0]+list(map(int, stdin.readline().strip())) # location 정보 받아오기: 앞에 0 추가하는 이유는 노드의 인덱스 번호를 1부터 시작하기 위해
graph = [[] for _ in range(n+1)] # 1번 노드부터 n번 노드까지 다 받아와야 하니
for _ in range(n-1): # 셋째 줄부터 n+1번 줄까지 받기
a, b = map(int, stdin.readline().split())
graph[a].append(b)
graph[b].append(a)
if location[a] == 1 and location[b] == 1: # 둘다 실내이면
ans +=2 # 서로 방문하는 케이스가 2가지이니 이걸 정답에 함께 바로 세는 걸로.
sum = 0
visited = [False] * (n+1)
for i in range(1, n+1):
if not visited[i] and location[i] == 0: # 실외인 애들을 기준으로
x = dfs(i, 0) # 현재 cnt = 0
sum += x*(x-1) #실외인 노드를 기준으로 인접 노드 애들 개수 세는 게 총 n*(n-1)이니 실외 노드 걸릴 때마다 이걸 전부 세기
print(sum + ans)참고 링크: https://kth990303.tistory.com/141
2. 위상 정렬 알고리즘
출처는 나동빈님 강의에서 가져왔다.(동빈님 강의 진심 강추..)
사이클이 없는 방향 그래프의 모든 노드를 방향성을 거스르지 않도록 순서대로 나열하는 알고리즘이다. 예를 들어 선수과목을 고려한 학습 순서를 설정한다고 하자.
2-1: 자료구조
2-2: 알고리즘(선행과목: 자료구조)
3-1: 고급 알고리즘(선행과목: 자료구조, 알고리즘)
이런 커리큘럼이 있다고 하면, 이 과목을 모두 듣는 적절한 순서는
자료구조 -> 알고리즘 -> 고급 알고리즘(O)
자료구조 -> 고급 알고리즘 -> 알고리즘(X)
이 될 것이다.
위상 정렬 알고리즘을 적용할 수 있으려면 전제 조건이 하나 있는데, 위에서 볼 수 있듯 1) 사이클이 존재하지 않고 2) 방향이 있어야 한다.
위에서 말했던 자구(1), 알고(2), 고급 알고(3)에 대한 위상 정렬을 도식화로 나타내보면 아래와 같다.

위상정렬에는 노드 간의 간선에 방향이 있기 때문에 위에서 보는 것과 같이 진입차수(Indegree)와 진출차수(Outdegree)가 존재한다.
- 진입차수: 특정한 노드로 들어오는 간선의 개수
- 진출차수: 특정한 노드에서 나가는 간선 개수
이제 위상 정렬에 해당될 때의 노드가 어떻게 배치되는지 위에서 확인했으니, 위상 정렬 알고리즘을 살펴보자. 위상 정렬 알고리즘을 구현하는 방법에는 여러가지가 있는데, 보통은 queue를 사용해 구현한다. 여기서는 큐를 이용한 위상정렬 알고리즘을 소개한다. 로직의 개요는 아래와 같다.
- for 문을 돌려 진입차수가 0인 모든 노드를 스캔해 큐에 넣는다.
- 큐가 빌 때까지(while queue) 아래 과정을 수행한다.
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드가 생기면 이를 큐에 append한다.
결과적으로 각 노드가 큐에 들어온 순서가 곧 위상 정렬을 수행한 결과와 같다.
여기서 배운 걸 그대로 예제를 풀면서 적용해보자. 문제는 줄 세우기(#2252)다. 위상 정렬을 공부하고 풀었을 때는 매우 쉽게 느껴져서 실버 4~5 정도 될까? 싶었는데 난이도가 골드 3이더라(;;;)
문제를 푸는 과정은 위상정렬을 공부했다면 간단하다.
먼저 n, m으로 사람 수와 키재는 횟수를 받는다.
이후에 키를 잴 때 두 사람의 번호를 받는데, 앞에 들어오는 번호가 뒤에 받는 번호보다 앞에 있으니 위상 정렬 관점에서 앞 번호를 인덱스, 뒷 번호를 해당 인덱스의 밸류로 저장한다. 여기까지 먼저 코드로 짜보면 아래와 같이 나타낼 수 있다. 앞에 받는 번호가 a, 뒷 번호가 b이니 height라는 이차원 배열을 하나 만들고 각 인덱스에 값을 append해서 저장한다.
b가 a 뒤에 서 있으니, 이 역시 위상 정렬 관점에서 a->b 이고 b의 진입차수가 1 올라간다. 따라서 indegree[b] +=1을 해준다.
from sys import stdin
from collections import deque
n, m = map(int, stdin.readline().split())
indegree = [0] * (n+1)
height = [[] for _ in range(n+1)]
for i in range(m):
a, b = map(int, stdin.readline().split())
height[a].append(b)
indegree[b] += 1
다음은 위상정렬 알고리즘에 대한 함수를 짠다. 위에서 설명했듯, 최종 키 순서를 담을 빈 리스트(result)와 진입차수가 0인 노드를 줄세울 queue를 하나 만든다.
모든 번호의 학생을 for문으로 쭉 스캔해 어느 누구 뒤에도 서 있지 않은 (즉, 자기한테 화살표를 쏘지 않는=진입차수가 0인) 애들을 스캔한다음 q에 추가한다.
while문을 돌면서 q에서 하나씩 popleft한 뒤, 해당 학생을 가장 맨 앞줄에 세운다(=result 리스트에서 가장 먼저 append). 이후, 해당 q에서 뽑은 학생 뒤에 서있는 애들을 줄줄이 불러와서 진입차수를 1씩 내린다. 이를 반복하면 indegree == 0이 나오는 애들이 하나둘씩 생겨날텐데 걔네들을 result에다가 계속 추가해준다. 가장 맨 앞에 서 있는 애를 먼저 줄 세우고 그 뒤에 서있는 애들을 하나씩 키를 깎으면서 데려오는 느낌이라고 생각하면 될듯?
전체 코드는 아래에.
from sys import stdin
from collections import deque
n, m = map(int, stdin.readline().split())
indegree = [0] * (n+1)
height = [[] for _ in range(n+1)]
for i in range(m):
a, b = map(int, stdin.readline().split())
height[a].append(b)
indegree[b] += 1
def topology_sort():
result = []
q = deque()
for i in range(1, n+1):
if indegree[i] == 0:
q.append(i)
while q:
now = q.popleft()
result.append(now)
for i in height[now]:
indegree[i] -= 1
if indegree[i] == 0:
q.append(i)
for i in result:
print(i, end=" ")
return
print(topology_sort())
'정글사관학교 개발일지 > 자료구조&알고리즘' 카테고리의 다른 글
| [자주 찾는 파이썬 기능 모음]Python 문자열 리스트 숫자로 변환 (0) | 2021.11.24 |
|---|---|
| 정글사관학교 23일차 TIL: 플로이드 와샬, 동전 2(#2294) (0) | 2021.11.24 |
| 정글사관학교 20일차 TIL: 크루스칼 알고리즘 (0) | 2021.11.21 |
| 정글사관학교 19일차 TIL: 트리 순회, 이진 검색 트리, Union-Find(유니온 파인드) 알고리즘 (0) | 2021.11.20 |
| 정글사관학교 18일차 TIL: MOO 게임(#5904), 문자열 폭발(#9935), 스카이라인(#1933) (0) | 2021.11.19 |