드디어 4주 간의 알고리즘 커리큘럼이 끝나는 날. 시원섭섭하다. 드디어 끝나서 후련한 마음 반, 지금부터 본격적으로 빡센 일정인 C언어 기반 커리큘럼이 다가왔다는 사실에 두려움 반. 하지만 그 알고리즘마저 해낸 마당에, 앞으로도 지금처럼 꾸역꾸역 하면 어떻게든 하겠지. 알고리즘 커리는 오늘로 끝이지만 앞으로 매일 한 문제씩 꼬박꼬박 풀 예정. 꾸준히 리뷰해야겠다. 이제 알고리즘 풀이 리뷰는 따로 카테고리를 만들어서 올릴 예정.
1. 계단 오르기(#2579)
마침 어제 풀었던 문제가 시험에 나와서 아주 기분 좋게 풀었더랬다. dp를 처음 계단을 오를 때 기점으로 생각하는 게 아니라 n번째 계단에 도착했을 때를 기점으로 거꾸로 생각하면 훨씬 간단하게 풀 수 있다. 아래 그림을 보자. n번째 계단에 도착하는 경우를 생각해보면 크게 두 가지 경우밖에 없다.
- n-2번째 계단에서 2칸 올라서 도착
- n-1번째 계단에서 1칸 올라서 도착
그런데 2번의 경우, n-1번째 계단에 도착해서 올라가기 위해서는 반드시 n-3번째 계단에서 2칸 올라서 n-1번째 계단에 도착해야 한다. 여기서 헷갈렸던 게, "엇? 이러면 n-2=> n-1 => n으로 올라가는 경우는 배제되는 거 아닌가?" 였다. 그런데 이 경우는 계단을 세 칸 연속 올라서는 케이스이기 때문에 될 수 없는 경우이다. 점프를 두 번 해서 이것도 된다고 생각했는데, 점프가 핵심이 아니라 밟는 계단이 연속 세 칸이기 때문에 되지 않는다는 것. 따라서 n-1번째 계단에 도착하려면 반드시 n-3번째 계단에서 2칸 올라서는 경우밖에 없다. 이것만 이해하면 점화식은 간단해진다.
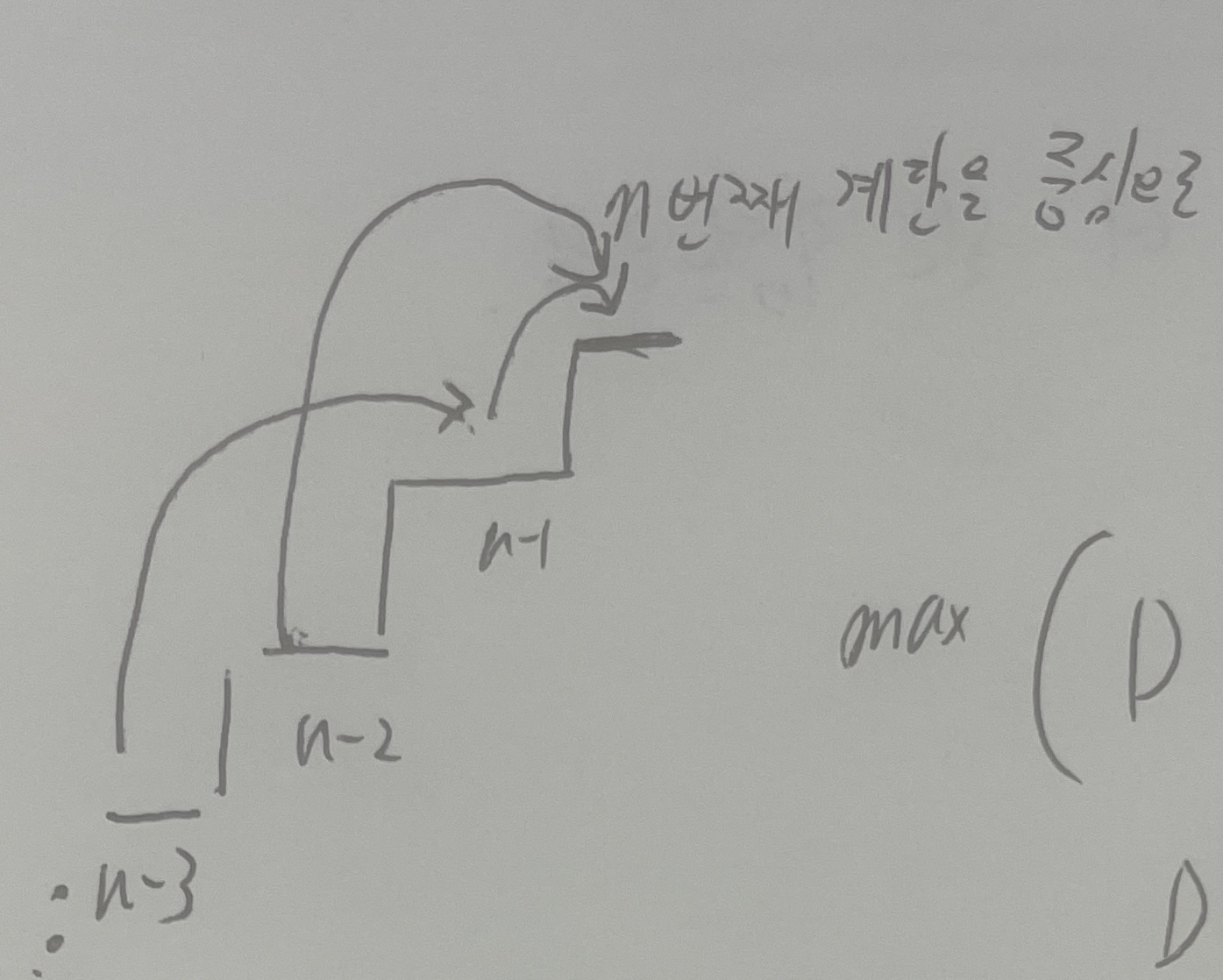
점화식: dp[i] = max(dp[i-3] + stairs[i-1] + stairs[i], dp[i-2]+stairs[i])
이를 코드로 짜면 다음과 같다. N의 크기가 1, 2, 3일 때는 위처럼 점화식을 짤 수 없으니 따로 return 값을 지정해주면 끝.
from sys import stdin
input = stdin.readline
N = int(input())
stairs = [int(input().strip()) for _ in range(N)]
dp = [0] * N
def upstairs():
if N == 1:
return stairs[0]
elif N == 2:
return max(stairs[0] + stairs[1], stairs[1])
elif N == 3:
return max(stairs[1]+stairs[2], stairs[0] + stairs[2])
dp[0] = stairs[0]
dp[1] = max(stairs[0] + stairs[1], stairs[1])
dp[2] = max(stairs[1]+stairs[2], stairs[0] + stairs[2])
for i in range(3, N):
dp[i] = max(dp[i-3] + stairs[i-1] + stairs[i], dp[i-2]+stairs[i])
return dp[-1]
print(upstairs())2. 내리막길(#1520)
이 문제는 시간초과로 씨름하다가 결국 해결하지 못했다. dp를 생각하지 않고 dfs로만 풀려고 하다보니 계속 문제가 발생했던 건데, 문제는 visited로 이미 dp와 비슷하게 구현하고 있는 게 아닌가 하는 생각에 무엇이 틀린 것인지 명확히 이해하지 못했다는 점. 그나마 dfs는 명확히 구현했으니 반은 맞췄다는데 의의를 두..고 싶지만 쨌든 틀린 건 틀린 거니 풀이 진행.
이 문제는 방문한 칸을 다시 방문하지 않는게 메인 로직이 아니다. visited를 쓰지 않고, 이차원 배열 dp를 만든다.
dp[i][j]: path[i][j]까지 가는 경우의 수라고 하자. 아직 가지 않은 초기화 상태를 만들기 위해 모든 dp 값에 -1을 넣는다. 이때, 0이 아닌 -1을 넣는 이유는 dp의 정의가 경우의 수이기 때문에 이 길로 가는 경우가 0인 케이스도 발생할 수 있어서이다. 즉, 가는 길이 없어서 0인 것과 아직 방문하지 않아서 0인 것을 혼동할 수 있기 때문에 경우의 수로 절대 나올 수 없는 값인 -1을 초기화 상태로 배정하는 것.
이 dp 배열에 대해 우리가 인지해야 하는 것은
dp[i][j] 값이
- dp[i][j] = 0이면 목적지까지 갈 수 있는 경우의 수가 0이라는 뜻이므로 0을 return한다.
- dp[i][j] = 1 이상의 값이면 이전에 연산한 방문 경로가 있다는 말이니 해당 값(경우의 수)을 더해서 반환해서 더해준다.
- dp[i][j] = -1이면 아직 방문하지 않은 경로라는 뜻이니 dfs + dp를 계속 진행한다.
이를 코드로 짜면 아래와 같다. (아래 코드에서는 dp를 visited로 적었으나 기능은 dp.)
from sys import stdin, setrecursionlimit
setrecursionlimit(10**9)
input = stdin.readline
M, N = map(int, input().split())
path = [list(map(int, input().split())) for _ in range(M)]
visited = [[-1] * N for _ in range(M)]
cnt = 0
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def dfs(y, x):
global cnt
if x == N-1 and y == M-1:
return 1
if visited[y][x] != -1:
return visited[y][x]
#방문
visited[y][x] = 0
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < N and 0 <= ny < M:
if path[y][x] > path[ny][nx]:
visited[y][x] += dfs(ny, nx)
return visited[y][x]
print(dfs(0, 0))
3. C언어 기초(ch.1 - ch.4)
드디어 C언어...! 기분이 싱숭생숭한데 생각보다 처음은 무난하다. 확실히 파이썬으로 언어 기초를 익혀놓으니 아직까지는 좀 더 쳐야 해서 불편한 것 빼고는 무난. 강의는 현재 나동빈님 C언어 프로그래밍 기초 강의를 듣는 중. 중요한 것 위주로만 정리.
ch.1
sizeof: 해당 변수의 메모리 크기를 반환하는 내장 함수
ch.2: 변수와 상수
C언어에서는 변수를 지정할 때, 항상 그 변수의 타입을 지정해줘야 한다. 예컨대 변수 x의 타입이 정수형이면 int x = 20; 이런 식으로. 아직 배우지 않았으나 함수 역시 마찬가지인 것으로 보이는데, 정수형 함수? 를 지칭하는 건지는 모르겠으나 int main(){}이라는 형태의 함수를 짤 때는 반드시 return 값으로 정수를 넣어주는 것으로 보인다.. 하지만 지금 강의에서는 초기 연습용으로 int를 쓰고 있어서 return 값을 0으로 반환하게 설정하고 본 목적은 printf를 호출하는 기능으로만 쓰는 것 같다. 그러니까, void 형태의 함수를 대신해서 int로 쓰는 것 같다. 파이썬 느낌으로 말하면, def 함수에서 return 값은 지정하지 않은 채 함수 내에서 print를 실행하기 위한 용도로 함수를 갖다 쓰는 느낌이랄까. 아래 코드를 보면 무슨 말인지 이해가 될 것이다.
#include <stdio.h>
int main(void){
int x = 20;
int y = 30;
printf("x = %d입니다.\n", x);
printf("y = %d입니다.\n", y);
printf("x + y = %d입니다.\n", x + y);
printf("x - y = %d입니다.\n", x - y);
printf("x * y = %d입니다.\n", x * y);
printf("x / y = %d입니다.\n", x / y);
return 0;
}
오버플로우에 대해서도 알아봤는데, 오버플로우는 컴퓨터에서 출력할 수 있는 정수의 최댓값을 넘어서는 값을 출력하게 했을 때 -(최댓값+a)를 출력하는 상황을 말한다. 이는 32비트 혹은 64비트 운영체제에서 한 번에 출력할 수 있는 정수의 최댓값이 정해져 있기 때문이다.(숫자를 비트로 계산하기 때문에)
#include <stdio.h>
#include <limits.h>
int main(void){
int x = INT_MAX;
printf("int형의 최댓값 x는 %d입니다.\n", x);
printf("x+1은 %d입니다.\n", x+1);
return 0;
}
// -(x+1)이 출력됨C언어에서는 정수형 변수를 지정하는 함수로 float과 double 두 가지가 있다. 둘의 차이는 정밀도에 있는데,
float: 소수점 이하 6자리 (4바이트 크기)
double: 소수점 이하 12자리 (8바이트 크기)
C언어에서 일반적인 실수 표현은 double 형식으로 취급한다. 그래서 float형식으로 반환하려면 실수 뒤에 f를 붙인다. 그래서 보통 0.1f, 0.2f 이런 식으로 덧붙여서 출력하게끔 하는데 이는 소수점 이하 몇 번째 자리까지 출력할 것인지를 지정하는 함수?이다. 그래서 double로 표기된 숫자가 메모리에서 차지하는 용량은 8 bytes이나 f가 붙으면 용량이 줄어든다.
ex)
sizeof(0.1) = 8 bytes
sizeof(0.1f) = 4 bytes
#include <stdio.h>
int main(void){
int x = 50;
float y = 123456789.123456789;
double z = 123456789.123456789;
printf("x = %d\n", x);
printf("y = %.2f\n", y);
printf("z = %.2f\n", z);
}
ch.3
진법에 따른 출력 방법에 대해서 배웠다. 기본적으로 우리가 %d라고 쓰는 건 십진수(decimal)의 형태로 출력하라는 의미를 담고 있다. 이를 8진수, 혹은 16진수로 출력하는 방법은 각각 %o, %x를 붙여서 출력하면 된다.
#include <stdio.h>
int main(void){
int x = 100;
printf("10진수로 출력: %d\n", x);
printf("8진수로 출력: %o\n", x);
printf("16진수로 출력: %x\n", x);
return 0;
}
C에서는 변수를 상수처럼 사용할 때 코드 상단에 define을 이용해서 특정 변수의 값을 고정시켜 사용할 수 있다. 사용하는 방식은
#define (변수 이름) (상수값)
예를 들어 내가 MONTHS라는 값을 12로 늘 일정하게 사용하고 싶다면 #define MONTHS 12 이렇게 치면 된다. 아래 코드를 보자.
#include <stdio.h>
#define MONTHS 12
int main(void){
double monthSalary = 1000.5;
printf("$ %.2f", monthSalary * MONTHS);
return 0;
}
Ch.4
연산자 중에 ++, -- 이런 것들을 굉장히 자주 보는데 이 의미는 1을 더하거나 뺀다는 말이다. 그런데 연산자의 위치에 따라 출력하는 값이 완전히 달라진다. 아래 코드를 보자. x++ 는 방금 말한 것처럼 1을 더한다는 뜻이니 x+1을 출력한다. 따라서 두 번째 줄에는 0+1=1을 출력한다.
이때, 그 다음 줄에 x--가 오는 것을 볼 수 있는데, 앞서 말한 것을 생각해보면 그 윗줄에서 +1을 했으니 1이었다가 두번째 printf에서 x--를 %d에 출력하도록 했으니 1-0 = 0이 나와야 하는 것이 아닌가? 여기서 연산자의 위치가 중요하다는 게 나온다. 현재 printf에서는 연산자가 x 뒤에 오기 때문에 두 번째 printf에서는 x++까지 계산한 값을 출력하고 그 다음 줄에서 x--가 적용된 값을 출력한다.
반면, 마지막 printf를 보면 --x로 쓰여있는 것을 볼 수 있다. 이는 앞의 x값에 -1만큼 빼라는 뜻은 똑같으나 연산자가 앞에 오기 때문에 그 줄에서 바로 -1을 계산한 값을 출력한다.
#include <stdio.h>
int main(void){
int x = 0;
printf("현재의 x는 %d입니다.\n", x);
x++;
printf("현재의 x는 %d입니다.\n", x--);
printf("현재의 x는 %d입니다.\n", x);
printf("현재의 x는 %d입니다.\n", --x);
return 0;
}
'정글사관학교 개발일지 > 자료구조&알고리즘' 카테고리의 다른 글
| 정글사관학교 33일차 TIL: C언어 기초 - 포인터, 함수 (0) | 2021.12.04 |
|---|---|
| 정글사관학교 32일차 TIL: C언어 기초(문자 입력, 포인터) (0) | 2021.12.04 |
| 정글사관학교 30일차 TIL: 코치님의 조언, 행렬 곱셈 순서(#11049) (0) | 2021.12.01 |
| 정글사관학교 29일차 TIL: 점프(#2253), 멀티탭 스케쥴링(#1700) (0) | 2021.11.30 |
| 정글사관학교 27일차 TIL: 외판원 순회 문제(TSP) -1 (0) | 2021.11.27 |